The Bayes-Duality Project

Toward AI that learns adaptively, robustly, and continuously, like humans

About People Research Publications

News

About the project

Goal: To develop a new learning paradigm for Artificial Intelligence (AI) that learns like humans in an adaptive, robust, and continuous fashion.

Summary: The new learning paradigm will be based on a new principle of machine learning, which we call the Bayes-Duality principle and will develop during this project. Conceptually, the new principle hinges on the fundamental idea that an AI should be capable of efficiently preserving and acquiring the relevant past knowledge, for a quick adaptation in the future. We will apply the principle to representation of the past knowledge, faithful transfer to new situations, and collection of new knowledge whenever necessary. Current Deep-learning methods lack these mechanisms and instead focus on brute-force data collection and training. Bayes-Duality aims to fix these deficiencies.

Funding and Duration:

Top

People

Team PIs

Approx-Bayes team
Emtiyaz Khan
Emtiyaz Khan

Research director (Japan side)

Approx-Bayes team at RIKEN-AIP and OIST

Stat-Theory team
Julyan Arbel
Julyan Arbel

Research director (France side)

Statify-team, Inria Grenoble Rhône-Alpes

Math-Science team
Kenichi Bannai
Kenichi Bannai

Co-PI (Japan side)

Math-Science Team at RIKEN-AIP and Keio University

HPC team
Rio Yokota
Rio Yokota

Co-PI
(Japan side)

Tokyo Institute of Technology

Core members

Pierre Alquier
Pierre Alquier

Core Member

(previously Research Scientist, Approx-Bayes team at RIKEN-AIP)

Thomas Moellenhoff
Thomas Möllenhoff

Core Member

Post-doc, Approx-Bayes team at RIKEN-AIP

Gian Maria Marconi
Gian Maria Marconi

Core Member

(previously a Post-doc, Approx-Bayes team at RIKEN-AIP)

Collaborators

Name University Position Team in project
Benoît Collins Kyoto University Professor Math-Science team
Florence Forbes Inria Grenoble Rhône-Alpes Principal investigator Stat-Theory team
Kei Hagihara RIKEN AIP Postdoctoral Researcher Math-Science team
Samuel Kaski University of Aalto Department of Computer Science, Professor Approx-Bayes team
Takahiro Katagiri Nagoya University, Information Technology Center Professor HPC team
Akihiro Ida The University of Tokyo, Information Technology Center, Project Associate Professor HPC team
Takeshi Iwashita Hokkaido University, Information Initiative Center Professor HPC team
Julien Mairal Inria Grenoble Rhône-Alpes Research scientist Stat-Theory team
Eren Mehmet Kiral RIKEN AIP Special Postdoctoral Researcher Math-Science team
Kengo Nakajima The University of Tokyo, Information Technology Center Professor HPC team
Takeshi Ogita Tokyo Woman’s Christian University, School of Arts and Sciences Professor HPC team
Jan Peters TU Darmstadt Professor Approx-Bayes team
Judith Rousseau Université Paris-Dauphine & University of Oxford Professor Stat-Theory team
Haavard Rue King Abdullah University of Science and Technology, CEMSE division Professor Approx-Bayes team
Akiyoshi Sannai RIKEN AIP Research Scientist Math-Science team
Mark Schmidt University of British Columbia, Department of Computer Science Associate Professor Approx-Bayes team
Arno Solin University of Aalto, Department of Computer Science Assistant Professor Approx-Bayes team
Siddharth Swaroop Haarvard University Post-doc Approx-Bayes team
Asuka Takatsu Tokyo Metropolitan University Associate Professor Math-Science team
Koichi Tojo RIKEN AIP Special Postdoctoral Researcher Math-Science team
Richard Turner Cambridge University, UK, Department of Engineering Associate Professor Approx-Bayes team
Mariia Vladimirova Inria Grenoble Rhône-Alpes PhD Student Stat-Theory team
Pierre Wolinski Inria Grenoble Rhône-Alpes & University of Oxford Post-doctoral fellow Stat-Theory team
Shuji Yamamoto Keio University/RIKEN AIP Associate Professor Math-Science team

Top

Open Positions

Here, we list a few open positions. If interested, please send all inquiries to jobs-bayes-duality (at) googlegroups (dot) com, and indicate the location(s) and group(s) you are interested in.

Top

Research

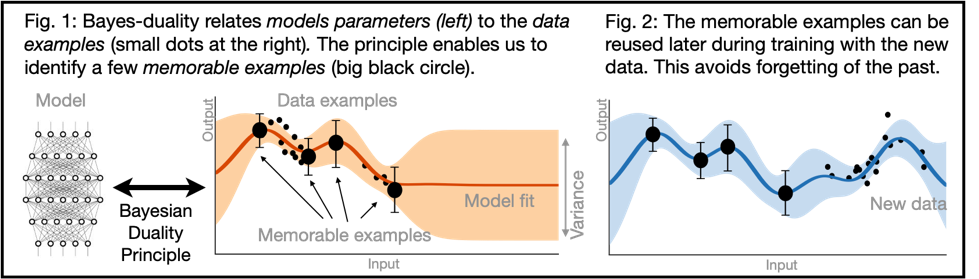
Bayes duality illustration

Our goal is to develop a new learning paradigm that enables adaptive, robust, and lifelong learning of AI systems. Deep learning methods are not sufficiently adaptive or robust, e.g., new knowledge cannot be easily added in trained models and, when forced, the old knowledge is easily forgotten. Given a new dataset, the whole model needs to be retrained from scratch on both the old and new data, and training only on the new dataset leads to the catastrophic forgetting of the past. All of the data must be available at the same time, which creates a dependency on large datasets and models that plagues almost all deep learning systems. Our main goal is to fix this by developing a new learning paradigm to support adaptive and robust systems that learn throughout their lives.

We introduce a new learning-principle for machine learning, which we call the Bayes Duality principle or “Bayes-Duality”. The principle exploits the “dual perspectives” of approximate (Bayesian) posteriors, to extend the concepts of duality (similar to convex duality) to nonconvex problems. It is based on a new discovery that natural-gradients used in approximate Bayesian methods automatically give rise to such dual representations. In the past, we have shown that natural-gradients for Bayesian problems yield a majority of machine learning algorithms as special cases (see our paper on the Bayesian Learning Rule). Our goal now is to show that the same approach to apply ideas of duality to nonconvex problems, such as those that arise in deep learning.

Our main goals in the future include the following:

  • A theory of Bayes-duality and connections to other dualities
  • Theoretical guarantees for adaptive systems based on Bayes-duality
  • Practical methods for knowledge transfer and collection in deep learning

Top

Publications

  • Variational Learning is Effective for Large Deep Networks,
    (ICML 2024) Y. Shen*, N. Daheim*, B. Cong, P. Nickl, G.M. Marconi, C. Bazan, R. Yokota, I. Gurevych, D. Cremers, M.E. Khan, T. Möllenhoff
    [ ArXiv ] [ Blog ] [ Code ] Accepted as Spotlight
  • Model Merging by Uncertainty-Based Gradient Matching,
    N. Daheim, T. Möllenhoff, E. M. Ponti, I. Gurevych, M.E. Khan [ ArXiv ]
  • Improving Continual Learning by Accurate Gradient Reconstructions of the Past,
    (TMLR) E. Daxberger, S. Swaroop, K. Osawa, R. Yokota, R. turner, J. M. Hernández-Lobato, M.E. Khan [ OpenReview ]
  • The Memory Perturbation Equation: Understanding Model’s Sensitivity to Data,
    (NeurIPS 2023) P. Nickl, L. Xu, D. Tailor, T. Möllenhoff, M.E. Khan [ arXiv ]
  • The fine print on tempered posteriors,
    (ACML 2023) K. Pitas, J. Arbel [ arXiv ]
  • Memory-Based Dual Gaussian Processes for Sequential Learning,
    (ICML 2023) P. E. Chang, P. Verma, S. T. John, A. Solin, M.E. Khan [ arXiv ]
  • Lie-Group Bayesian Learning Rule,
    (AISTATS 2023) E. M. Kiral T. Möllenhoff, M.E. Khan [ arXiv ]
  • SAM as an Optimal Relaxation of Bayes,
    (ICLR 2023) T. Möllenhoff, M.E. Khan [ arXiv ] [ Tweet ]
    Accepted for an oral presentation, 5% of accepted papers (75 out of 5000 submissions),
  • The Bayesian Learning Rule,
    (JMLR) M.E. Khan, H. Rue [ JMLR 2023 ] [ arXiv ] [ Tweet ]
  • Knowledge-Adaptation Priors,
    (NeurIPS 2021) M.E. Khan*, Siddharth Swaroop* [ arXiv ] [ Slides ] [ Tweet ] [ SlidesLive Video ]
  • Dual Parameterization of Sparse Variational Gaussian Processes,
    (NeurIPS 2021) P. Chang, V. ADAM, M.E. Khan, A. Solin [ arXiv ]
  • Continual Deep Learning by Functional Regularisation of Memorable Past,
    (NeurIPS 2020, Oral) P. Pan*, S. Swaroop*, A. Immer, R. Eschenhagen, R. E. Turner, M.E. Khan [ arXiv ] [ Code ] [ Poster ]
  • Approximate Inference Turns Deep Networks into Gaussian Processes,
    (NeurIPS 2019) M.E. Khan, A. Immer, E. Abedi, M. korzepa. [ arXiv ] [ Code ]
  • Decoupled Variational Gaussian Inference,
    (NIPS 2014) M.E. Khan [ Paper and appendix ]
  • Fast Dual Variational Inference for Non-Conjugate Latent Gaussian Models,
    (ICML 2013) M.E. Khan, A. Aravkin, M. Friedlander, M. Seeger [ Paper ]

Top